Most electronics engineers and technicians have a good understanding of total harmonic distortion (THD). But there are a few elusive details that come into play during THD measurements.
Slot Harmonics Define
THD is the ratio of the sum of the powers of all harmonic components to the power of the fundamental frequency. Properly speaking, the fundamental frequency is the first harmonic, but THD discussions frequently don't acknowledge this fact. THD considers distortion contributed by second-order and higher harmonics but not by the random frequency, broad-spectrum distortion that is known as noise. THD + noise is a separate though important metric.
The familiar sine wave is comprised of a single frequency, while non-sinusoidal waveforms are made up of two or more sine waves that can be added together on a point-by-point basis moving along the time-domain X-axis. Breaking down a complex non-sinusoidal waveform's sine wave components is a mathematically difficult process but became practical with the advent of the Fast Fourier Transform in the 1960s. Today, one simply imports the nonsinusoidal signal into a spectrum analyzer or, using Math Mode in an oscilloscope, presses FFT. Then, displayed on the screen in real time, is the signal at the channel input in the frequency domain.
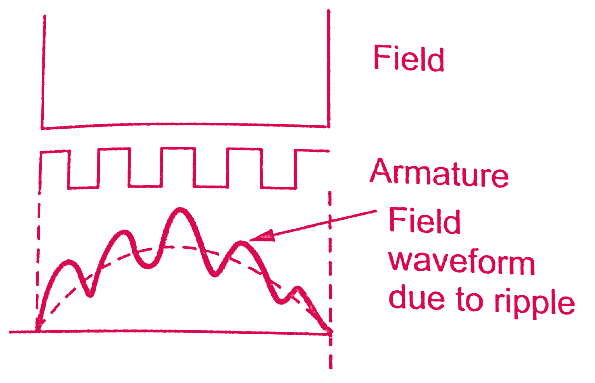
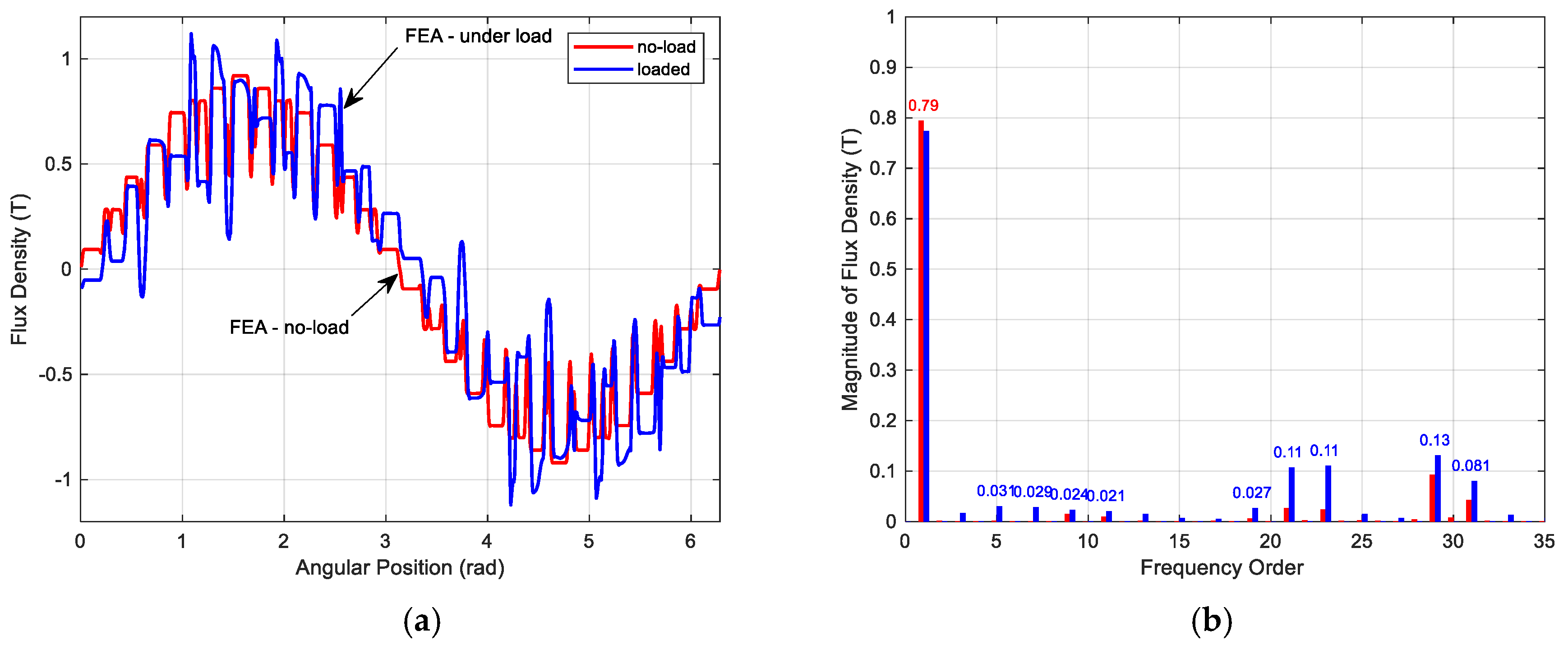
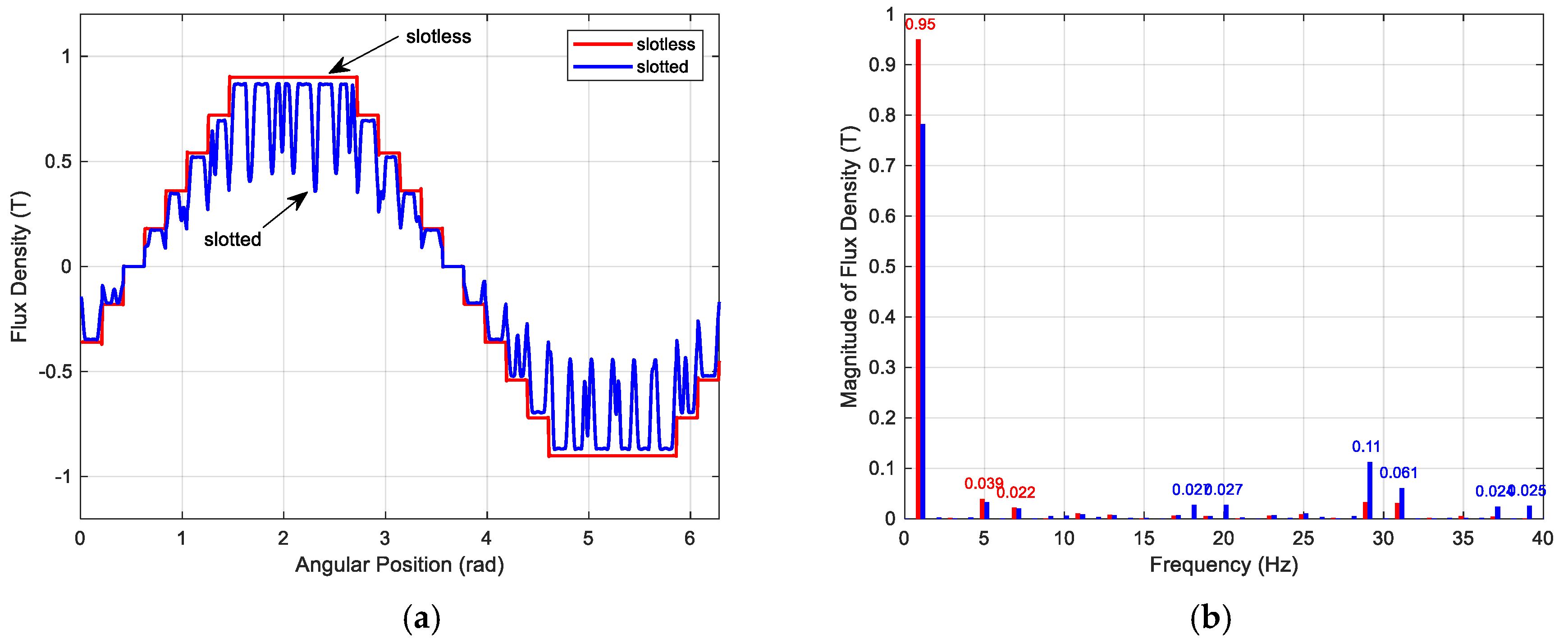
Frequencies of both the slot harmonics and synchronous torques Tables I-IV contain categories, slot-harmonic frequencies, and parasitic synchronous-torque frequencies for machines with pole-pairs ranging from p ¼ 1up to p ¼ 4; for chosen numbers of rotor slots N (denoted in the tables as 'NR'). These slot- harmonics are the source of a non-negligible part of the unbalanced magnetic pull (UMP). This paper presents analytical justifications for the use of a numerical impulse method to calculate the effects of the slot-harmonics on the UMP.
Amplitude, in units of power (dB) rather than volts, displays on the Y-axis and frequency, rather than time, displays along the Y-axis. These are the harmonics that, added together and divided by the fundamental, make up THD.
A high THD level in power systems is harmful for the system as well as for connected equipment. Lower THD equates to lower peak currents, higher efficiency and higher power factor.
Power factor is generally thought of as determined by the phase relationship between voltage and current, in accordance with: Power Factor PF = cos θv – cos θi, where θv is the phase angle of the voltage and θi is the phase angle of the current.
While this equation, known as the displacement factor, is valid when voltage and current are sinusoidal, it does not account for THD in non-sinusoidal circuits, which are prevalent today thanks to the rise of nonlinear loads with abundant harmonics.
Loads that include power conversion equipment — such as ac-dc, dc-ac and dc-dc, or nonlinear loads such as fluorescent ballasts — create a heavy nonlinear environment in which harmonics and THD abound. Switching power supplies, now common in office and home, contribute to this mix. This loading modifies the higher-quality sinusoidal power at the utility generator terminals. (Generators do contribute some fifth-order harmonics because of magnetic flux that takes place at the stator slots in addition to non-sinusoidal flux across the air gap.)
VFDs, welders and arc furnaces also generate prodigious amounts of THD.
Because harmonic currents are at higher frequencies that the power system fundamental, they see greater impedances. The cause of this strange phenomenon is that greater amounts of higher-frequency current flow near the surface of a conductor. With less usable cross-sectional area, the effective resistance of the conductor rises, resulting in more heat. This is seen in three-phase neutral conductors and transformer windings.
When an ac motor is powered by a VFD, it gets a powerful direct dose of harmonics. This is a consequence of the high-speed switching in the VFD inverter section. Most of the ambient harmonics caused by other nonlinear loads in the same building or neighborhood are not much of a problem because they generally get suppressed when the power goes through the dc bus midway through the VFD. These outside harmonics do, however, assault the many autonomous motors that are found in the workplace.
For one thing, harmonics create flux distribution in motor air gaps, causing poor start-ups and abnormally high slip in induction motors. A serious problem in motors and generators is pulsating torque, causing losses and mechanical oscillations with harmful heat.
Here's the greatest problem in motors when there is high THD riding on the good power at the input:
Because of the alternating magnetic field, there is a normal temperature rise in the iron core due to eddy current and hysteresis loss. That is a given, and the iron core is by design sufficiently massive to dissipate this heat. But as it happens, the amount of eddy current loss varies with the square of the frequency. When high-frequency harmonics come along, the heat rises dramatically and, as it dissipates, a significant portion migrates into the windings, adding to the excess heat generated there by the unwanted harmonics and further stressing the winding insulation. Hysteresis varies directly with the frequency, not with its square, but still, it adds to the total.
Another factor, even more harmful, is a loss within the windings. This source of heat varies with the square of the current (I2 Tournoi poker divonne novembre 2019. R) and the harmonics have a significant negative impact. Additionally, these high-frequency components exhibit harmful skin effect, reducing effective conductor size.
If a generator is to supply nonlinear loads, it should be derated because it has higher reactance and impedance than a similar size motor. Combined with high-frequency magnetic flux resulting from the presence of powerful harmonics, they boost the stator temperature. Rotor heating also results from these high-frequency currents.
Additionally, harmonics set the stage for often catastrophic transformer failure. Generally trouble-free, transformers without warning may explode as big nonlinear loads abruptly switch on. The problem is compounded in older transformers containing toxic PCB-laden cooling oil.
Copper and iron losses combine to create a hazardous situation. Eddy current rises when harmonics enter a transformer from line or load. Because eddy current is proportional to the square of the applied current and the square of its frequency, a transformer catastrophe can happen suddenly and without warning.
Harmonic current in transformers is a source of electromagnetic interference that can degrade nearby communication circuits. Shielding, increased spatial separation and suppression of the harmonics are used to mitigate these effects.
To summarize, Fourier analysis (as opposed to Fourier synthesis), of a periodic signal reveals the harmonic frequencies that are components and integer multiples of the signal. This is where THD appears.
The reason that a voltage and its associated current are purely sinusoidal is that they consist of a single frequency. Multiple higher frequency components contribute to the observed THD. A square wave has a great amount of this distortion while a sine wave that is in the real, non-ideal world has a small amount of it. In most cases, that component is not visible in the time domain, but it can usually be observed just above the noise floor in the frequency domain.
THD is a constant concern in power systems. Low power factor, higher peak currents and low efficiency accompany high THD. In audio reproduction, a low THD equates to better fidelity. In communications systems, high THD means a potential for interference with nearby equipment and greater power consumption at the transmitter.
A THD analyzer can be used to measure the distortion of a waveform in comparison to a distortion-free sine wave. The instrument breaks the wave under investigation into its harmonics and compares each harmonic to the fundamental. An alternate procedure is to remove the fundamental by means of a notch filter, then measuring the remaining signal which will be the THD plus noise.
In audio equipment development, a low-distortion arbitrary function generator is used to insert an input into the unit being evaluated. Distortion at constituent frequencies is then measured for comparison of prototypes. In such procedures, crossover distortion for any given THD level is more audible and thus tends to outweigh clipping distortion, which produces higher-order harmonics.
Generally, harmonics are beneficial only to the musician, who uses them in a flute or guitar to produce sounds that would otherwise be beyond the capability of the instrument.
The best way to mitigate harmonics is to suppress them at the source. An alternative is to create shielding or filters at the equipment that is affected by the harmonics. Then, measuring the amount of THD, the success of these measures can be evaluated.
You may also like:
In this article we will discuss about: 1. Definition of Harmonics 2. Harmonic Number (h) 3. Types 4. Causes.
Definition of Harmonics:
Harmonics are sinusoidal voltages or currents having frequencies that are integer multiples of the frequency at which the supply system is designed to operate.
Harmonics as pure tones making up a composite tone in music. A pure tone is a musical sound of a single frequency, and a combination of many pure tones makes up a composite sound. Sound waves are electromagnetic waves travelling through space as a periodic function of time. Can the principle behind pure music tones apply to other functions or quantities that are time dependent?
ADVERTISEMENTS:
In the early 1800s, French mathematician, Jean Baptiste Fourier formulated that a periodic non-sinusoidal function of a fundamental frequency f may be expressed as the sum of sinusoidal functions of frequencies which are multiples of the fundamental frequency. In our discussions here, we are mainly concerned with periodic functions of voltage and current due to their importance in the field of power quality. In other applications, the periodic function might refer to radiofrequency transmission, heat flow through a medium, vibrations of a mechanical structure, or the motions of a pendulum in a clock.
A sinusoidal voltage or current function that is dependent on time t may be represented by the following expressions:
Voltage function,
v(t) = V sin (ωt) …(4.1)
Current function,
i(t) = I sin (ωt ± θ) …(4.2)
where, ω = 2πf is known as the angular velocity of the periodic waveform and 0 is the difference in phase angle between the voltage and the current waveforms referred to as a common axis. The sign of phase angle θ is positive if the current leads the voltage and negative if the current lags the voltage.
Figure 4.1 contains voltage and current waveforms expressed by Eqs. (4.1) and (4.2) and which by definition are pure sinusoids.
Slot Harmonics Means Test
For the periodic non-sinusoidal waveform shown in Fig. 4.2, the simplified Fourier expression states-
V (t) = V0 + V1 sin(ωt) + V2 sin(2 ωt) + V3 sin(3 ωt) + … + Vn sin( n ωt) + Vn+1 sin (( n + 1) ωt) +…………. (4.3)
The Fourier expression is an infinite series. In this equation, V0 represents the constant or the DC component of the waveform.
V1, V2, V3, … , Vn are the peak values of the successive terms of the expression. The terms are known as the harmonics of the periodic waveform. The fundamental (or first harmonic) frequency has a frequency of f, the second harmonic has a frequency of 2 x f, the third harmonic has a frequency of 3 x f, and the nth harmonic has a frequency of n x f. If the fundamental frequency is 60 Hz (as in the U.S.), the second harmonic frequency is 120 Hz, and the third harmonic frequency is 180 Hz.
The significance of harmonic frequencies can be seen in Fig. 4.3. The second harmonic undergoes two complete cycles during one cycle of the fundamental frequency, and the third harmonic traverses three complete cycles during one cycle of the fundamental frequency.
The best way to mitigate harmonics is to suppress them at the source. An alternative is to create shielding or filters at the equipment that is affected by the harmonics. Then, measuring the amount of THD, the success of these measures can be evaluated.
You may also like:
In this article we will discuss about: 1. Definition of Harmonics 2. Harmonic Number (h) 3. Types 4. Causes.
Definition of Harmonics:
Harmonics are sinusoidal voltages or currents having frequencies that are integer multiples of the frequency at which the supply system is designed to operate.
Harmonics as pure tones making up a composite tone in music. A pure tone is a musical sound of a single frequency, and a combination of many pure tones makes up a composite sound. Sound waves are electromagnetic waves travelling through space as a periodic function of time. Can the principle behind pure music tones apply to other functions or quantities that are time dependent?
ADVERTISEMENTS:
In the early 1800s, French mathematician, Jean Baptiste Fourier formulated that a periodic non-sinusoidal function of a fundamental frequency f may be expressed as the sum of sinusoidal functions of frequencies which are multiples of the fundamental frequency. In our discussions here, we are mainly concerned with periodic functions of voltage and current due to their importance in the field of power quality. In other applications, the periodic function might refer to radiofrequency transmission, heat flow through a medium, vibrations of a mechanical structure, or the motions of a pendulum in a clock.
A sinusoidal voltage or current function that is dependent on time t may be represented by the following expressions:
Voltage function,
v(t) = V sin (ωt) …(4.1)
Current function,
i(t) = I sin (ωt ± θ) …(4.2)
where, ω = 2πf is known as the angular velocity of the periodic waveform and 0 is the difference in phase angle between the voltage and the current waveforms referred to as a common axis. The sign of phase angle θ is positive if the current leads the voltage and negative if the current lags the voltage.
Figure 4.1 contains voltage and current waveforms expressed by Eqs. (4.1) and (4.2) and which by definition are pure sinusoids.
Slot Harmonics Means Test
For the periodic non-sinusoidal waveform shown in Fig. 4.2, the simplified Fourier expression states-
V (t) = V0 + V1 sin(ωt) + V2 sin(2 ωt) + V3 sin(3 ωt) + … + Vn sin( n ωt) + Vn+1 sin (( n + 1) ωt) +…………. (4.3)
The Fourier expression is an infinite series. In this equation, V0 represents the constant or the DC component of the waveform.
V1, V2, V3, … , Vn are the peak values of the successive terms of the expression. The terms are known as the harmonics of the periodic waveform. The fundamental (or first harmonic) frequency has a frequency of f, the second harmonic has a frequency of 2 x f, the third harmonic has a frequency of 3 x f, and the nth harmonic has a frequency of n x f. If the fundamental frequency is 60 Hz (as in the U.S.), the second harmonic frequency is 120 Hz, and the third harmonic frequency is 180 Hz.
The significance of harmonic frequencies can be seen in Fig. 4.3. The second harmonic undergoes two complete cycles during one cycle of the fundamental frequency, and the third harmonic traverses three complete cycles during one cycle of the fundamental frequency.
V1, V2, and V3 are the peak values of the harmonic components that comprise the composite waveform, which also has a frequency of f.
The ability to express a non-sinusoidal waveform as a sum of sinusoidal waves allows us to use the more common mathematical expressions and formulas to solve power system problems. In order to find the effect of a non-sinusoidal voltage or current on a piece of equipment, we only need to determine the effect of the individual harmonics and then vectorially sum the results to derive the net effect. Figure 4.4 illustrates how individual harmonics that are sinusoidal can be added to form a non-sinusoidal waveform.
The Fourier expression in Eq. (4.3) has been simplified to clarify the concept behind harmonic frequency components in a nonlinear periodic function. For the purist, the following more precise expression is offered. For a periodic voltage wave with fundamental frequency of-
ω = 2πf,
v(t) = V0 + ∑(ak cos kωt + bk sin k ωr) (for k- 1 to ∞)…(4.4)
Where ak and bk are the coefficients of the individual harmonic terms or components. Under certain conditions, the cosine or sine terms can vanish, giving us a simpler expression. If the function is an even function, meaning f (-t) = f(t), then the sine terms vanish from the expression. If the function is odd, with f (- t) = – f(t) then the cosine terms disappear.
For our analysis, we will use the simplified expression involving sine terms only. It should be noted that having both sine and cosine terms affects only the displacement angle of the harmonic components and the shape of the nonlinear wave and does not alter the principle behind application of the Fourier series. The coefficients of the harmonic terms of a function-
f(t) contained in Eq. (4.4) are determined by- Coefficient
The coefficients represent the peak values of the individual harmonic frequency terms of the nonlinear periodic function represented by f (t).
Harmonic Number (h):
Harmonic number (h) refers to the individual frequency elements that comprise a composite waveform. For example, h = 3 refers to the third harmonic component with a frequency equal to third times the fundamental frequency. Poker chasing losses. If the fundamental frequency is 60 Hz, then the 3rd (third) harmonic frequency is 3 x 60, or 180 Hz. The harmonic number 6 is a component with a frequency of 360 Hz.
Dealing with harmonic numbers and not with harmonic frequencies is done for two reasons. The fundamental frequency varies among individual countries and applications. The fundamental frequency in the U.S. is 60 Hz, whereas in Europe and many Asian countries it is 50 Hz. Also, some applications use frequencies other than 50 or 60 Hz; for example, 400 Hz is a common frequency in the aerospace industry, while some AC systems for electric traction use 25 Hz as the frequency.
The inverter part of an AC adjustable speed drive can operate at any frequency between zero and its full rated maximum frequency, and the fundamental frequency then becomes the frequency at which the motor is operating. The use of harmonic numbers allows us to simplify how we express harmonics. The second reason for using harmonic numbers is the simplification realized in performing mathematical operations involving harmonics.
Types of Harmonics:
Odd and Even Order Harmonics:
As their names imply, odd harmonics have odd numbers (e.g., 3, 5, 7, 9, 11), and even harmonics have even numbers (e.g., 2, 4, 6, 8, 10). Harmonic number 1 is assigned to the fundamental frequency component of the periodic wave. Harmonic number 0 represents the constant or DC component of the waveform. The DC component is the net difference between the positive and negative halves of one complete waveform cycle.
Figure 4.5 shows a periodic waveform with net DC content. The DC component of a waveform has undesirable effects, particularly on transformers, due to the phenomenon of core saturation. Saturation of the core is caused by operating the core at magnetic field levels above the knee of the magnetization curve. Transformers are designed to operate below the knee portion of the curve.
When DC voltages or currents are applied to the transformer winding, large DC magnetic fields are set up in the transformer core. The sum of the AC and the DC magnetic fields can shift the transformer operation into regions past the knee of the saturation curve. Operation in the saturation region places large excitation power requirements on the power system. The transformer losses are substantially increased, causing excessive temperature rise. Core vibration becomes more pronounced as a result of operation in the saturation region.
We usually look at harmonics as integers, but some applications produce harmonic voltages and currents that are not integers. Electric arc furnaces are examples of loads that generate non-integer harmonics. Arc welders can also generate non-integer harmonics. In both cases, once the arc stabilizes, the non-integer harmonics mostly disappear, leaving only the integer harmonics.
The majority of nonlinear loads produce harmonics that are odd multiples of the fundamental frequency. Certain conditions need to exist for production of even harmonics. Uneven current draw between the positive and negative halves of one cycle of operation can generate even harmonics. The uneven operation may be due to the nature of the application or could indicate problems with the load circuitry. Transformer magnetizing currents contain appreciable levels of even harmonic components and so do arc furnaces during startup. Sub-harmonics have frequencies below the fundamental frequency and are rare in power systems.
When sub-harmonics are present, the underlying cause is resonance between the harmonic currents or voltages with the power system capacitance and inductance. Sub-harmonics may be generated when a system is highly inductive (such as an arc furnace during startup) or if the power system also contains large capacitor banks for power factor correction or filtering. Such conditions produce slow oscillations that are relatively un-damped, resulting in voltage sags and light flicker.
Causes of Voltage and Current Harmonics:
A pure sinusoidal waveform with zero harmonic distortion is a hypothetical quantity and not a practical one. The voltage waveform, even at the point of generation, contains a small amount of distortion due to non-uniformity in the excitation magnetic field and discrete spatial distribution of coils around the generator stator slots. The distortion at the point of generation is usually very low, typically less than 1.0%.
The generated voltage is transmitted many hundreds of miles, transformed to several levels, and ultimately distributed to the power user. The user equipment generates currents that are rich in harmonic frequency components, especially in large commercial or industrial installations. As harmonic currents travel to the power source, the current distortion results in additional voltage distortion due to impedance voltages associated with the various power distribution equipment, such as transmission and distribution lines, transformers, cables, buses, and so on.
Figure 4.9 illustrates how current distortion is transformed into voltage distortion. Not all voltage distortion, however, is due to the flow of distorted current through the power system impedance. For instance, static uninterruptible power source (UPS) systems can generate appreciable voltage distortion due to the nature of their operation. Normal AC voltage is converted to DC and then reconverted to AC in the inverter section of the UPS. Unless waveform shaping circuitry is provided, the voltage waveforms generated in UPS units tend to be distorted.
As nonlinear loads are propagated into the power system, voltage distortions are introduced which become greater moving from the source to the load because of the circuit impedances. Current distortions for the most part are caused by loads. Even loads that are linear will generate nonlinear currents if the supply voltage waveform is significantly distorted.
When several power users share a common power line, the voltage distortion produced by harmonic current injection of one user can affect the other users. This is why standards are being issued that will limit the amount of harmonic currents that individual power users can feed into the source.
The major causes of current distortion are nonlinear loads due to adjustable speed drives, fluorescent lighting, rectifier banks, computer and data-processing loads, arc furnaces, and so on. One can easily visualize an environment where a wide spectrum of harmonic frequencies are generated and transmitted to other loads or other power users, thereby producing undesirable results throughout the system.